Can Matrix Determinant Be Negative
Minus b times the determinant of the matrix that is not in bs row or column. The Jacobian determinant at a given point gives important information about the behavior of f near that point.

Linear Algebra Ch 2 Determinants 8 Of 48 Example Of Rule 2 The Negative Of A Determinant 3x3 Youtube
The Hessian matrix of a convex function is positive semi-definiteRefining this property allows us to test whether a critical point is a local maximum local minimum or a saddle point as follows.
. The pattern continues for 44 matrices. Also it is used to find the inverse of a matrix. A matrix is a rectangular array of numbers variables symbols or expressions that are defined for the operations like subtraction addition and multiplications.
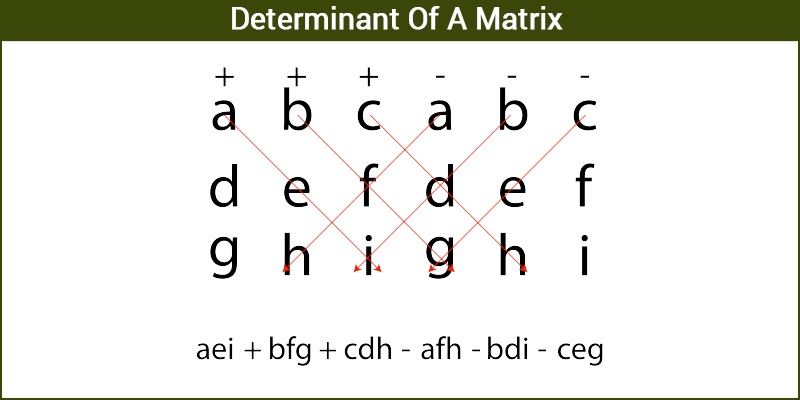
An easy method for calculating 3 X 3 determinants is found by rearranging and factoring the terms given above to get. If the determinant of a matrix is not equal to 0 then it is an invertible matrix as we can find its inverse. For 44 Matrices and Higher.
Each of the quantities in parentheses represents the determinant of a 2 X 2 matrix that is the part of the 3 x 3 matrix remaining when the row and column of the multiplier are. If the Hessian is positive-definite at then attains an isolated local minimum at. If a matrix order is in n x n then it is a square matrix.
So here 44 is a square matrix that has four rows and four columns. Minor of a Matrix. If m n then f is a function from R n to itself and the Jacobian matrix is a square matrixWe can then form its determinant known as the Jacobian determinantThe Jacobian determinant is sometimes simply referred to as the Jacobian.
Determinant of a 44 matrix is a unique number that is also calculated using a particular formula. Minus d times the determinant of the matrix that is not in ds row or column. The determinant of a matrix can be either positive negative or zero.
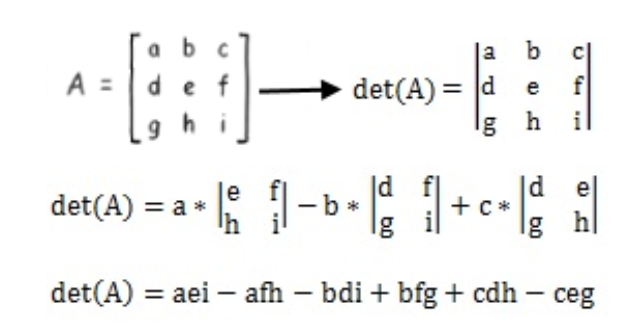
Plus a times the determinant of the matrix that is not in as row or column. Since the square of the determinant of a matrix can be found with the above formula and because this multiplication is defined for nonsquare matrices we can extend determinants to nonsquare matrices. The determinant of a matrix is equal to the determinant of its transpose.
The determinant of matrix is used in Cramers rule which is used to solve the system of equations. Plus c times the determinant of the matrix that is not in cs row or column. Introduction to Determinant of 4x4 Matrix.
The determinant of a 3 x 3 matrix A is defined as. For example take the 3 wide matrix A defined with column vectors x y and z where each have n components. If A is a square matrix then the determinant of the matrix A is.
The determinant of the product of two square matrices is equal to the product of the determinants of the given matrices. The determinant obtained through the elimination of some rows and columns in a square matrix is called a minor of that matrix. The size of a matrix which is known as the order of the matrix is determined by the number of rows and columns in the matrixThe order of a matrix with 6 rows and 4 columns is represented as a 6 4 and is read as 6 by 4.
For instance the continuously. If the Hessian is negative-definite at then attains an isolated local maximum at.
Properties Of Determinants Studypug

Linear Algebra Ch 2 Determinants 8 Of 48 Example Of Rule 2 The Negative Of A Determinant 3x3 Youtube

Determinant Of A Matrix Definition Higher Order Methods Video Example

How To Find The Determinant Of A Matrix Precalculus Study Com

Determinant Of A Matrix For Square Matrices With Examples
What Does A Negative Determinant Mean All Things Statistics
0 Response to "Can Matrix Determinant Be Negative"
Post a Comment